ATMOSPHERIC Optical Phenomena

Objectives:

Solar radiation, consisting of a range of wavelengths, interacts with matter in many ways. The wavelengths from about 0.4 to 0.7 micrometers (μm) are known as visible light because we sense them with our eyes. Visible light also interacts with the air, cloud and precipitation particles, and aerosols in several ways including scattering, reflection, and refraction. These optical effects can produce spectacular displays of light and color. These phenomena also give evidence of processes taking place in the atmosphere that may be harbingers of future weather.

After completing this investigation, you should be able to:

• Explain how light interacts with atmospheric water droplets and ice crystals to form rainbows and halos.
• Describe the implications of these optical phenomena for the state of the atmosphere.

Introduction:

As shown in Figure 1 at the right, when a light ray crosses an interface from one transparent medium to another (such as from air to water), the speed of light changes. If the angle of the light ray is other than perpendicular to the interface, the direction of motion in the new medium is also altered. This change of direction is described by Snell’s law which states that when a light ray passes into a medium in which the speed of light is slower, the light ray is bent toward the line perpendicular to the interface (Figure 1, ray passing from air to water). If light speeds up when it enters the second medium (Figure 1, ray passing from water to air) a light ray bends away from the perpendicular. Refraction is the bending of a light ray.

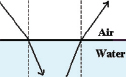
Figure 1. Bending of light rays crossing an interface.

For light passing from air (higher speed) into a hexagonal ice crystal (lower speed), the light ray is bent toward the crystal interior. In exiting from the crystal, it is refracted once more, but in reverse fashion. A hexagonal crystal has six rectangular sides, each of which adjoins adjacent sides at a 120-degree angle, and two ends (hexagonal in shape) which are positioned at a 90-degree angle to the sides. A refracted light ray follows one of two paths through a hexagonal ice crystal: through two sides, or a side and an end. The deflection angle of a ray passing through two sides is 22° from its original direction while that through a side and an end is 46° from its original direction.

Figure 2 approximates the orientation of ice crystals that would interact with light rays to form halos of 22° and 46° relative to the observer. The angle is measured where straight lines drawn from the center of the Sun (or Moon) and from the halo meet in the observer’s eye. Because ice crystals in the air are more or less randomly oriented, the combination of all the rays would appear as a circle about the light source. The 22° halo is seen when the light passes in and out of rectangular sides of the ice crystal. A similar process occurs for the 46° halo except the light passes through one side and one end of the crystal. Because there are six sides and only two ends to an ice crystal, probability favors seeing more 22° halos than the 46° kind. The 22° halo is also brighter.

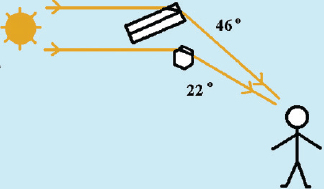
Figure 2. Light rays bent by ice crystals (not to scale).

1. As shown in Figure 2, the observer would need to look in the general direction [(toward)(away from)] the Sun to see a halo. (Caution: never look directly at the Sun! Sky observations near the Sun need eye protection or blockage of the Sun’s direct rays, such as with your hand.)

2. Halos indicate clouds that are composed of [(ice crystals)(liquid droplets)].

Figure 3 shows, from the perspective of the observer, the circular 22° and 46° halos about the sun position along with a sun pillar and parhelia (sundogs). A sun pillar is a bright column seen above and below the sun position. The pillar is caused by reflection of the sunlight from the upper and lower surfaces of ice crystals with surfaces oriented horizontally, much like looking at a streetlight through partially opened horizontal venetian blinds. This is best seen near sunrise or sunset when the atmosphere is stable and the larger surfaces of the crystals are horizontally oriented.

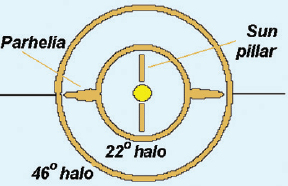
Figure 3. Halos, parhelia and sun pillar (not to scale).

3. Parhelia, commonly called sundogs or mock suns, are bright spots sometimes seen at and just outside the 22° halo circle at the same level as the Sun. The term “sundogs” refer to the dogs that followed the mythological chariot of Mercury, the sun god. Parhelia are primarily formed by the refraction of light passing through hexagonal plate crystals oriented with their relatively large top and bottom six-sided surfaces generally horizontal (falling much like single playing cards which remain horizontal after released from a horizontal position). Parhelia have some coloration caused by refraction of light through the crystals. The distance of parhelia from the Sun increases with increasing solar altitude; at solar altitudes greater than about 60 degrees, parhelia cannot be observed. Stable atmospheric conditions and the presence of horizontal ice crystal surfaces favor the appearance of parhelia and sun pillars, but only [(parhelia)(sun pillars)] require the passing of light through crystals.

4. Figure 4 suggests the orientation that raindrops would have to the Sun’s rays and the observer’s location for the formation of a rainbow. The color separation in the primary and secondary rainbows is formed from refraction of the ray both on entering and on leaving a drop. The longer wavelength red light is refracted slightly less than the shorter wavelength violet, resulting in the color separation. The primary rainbow has a single internal reflection of the ray whereas the secondary bow results from [(one)(two)(three)] reflections of the ray inside the drop.

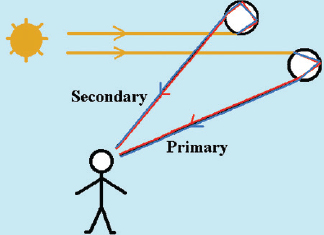
Figure 4. Rainbow formation (not to scale).

5. Rainbows would be seen by looking generally [(toward)(away from)] the Sun.

6. Observing a rainbow can provide weather forecasting hints. A rainbow seen in the morning would be produced by rain falling generally to the [(east)(west)] of the observer.

7. Because weather systems generally move from west to east, this bow-producing rainshower would move [(toward)(away from)] the observer. So, fair weather might be delayed.

8. In a similar way, a rainbow seen in the afternoon is a harbinger of [(stormy)(clearing)] weather to follow.

9. Because raindrops have curved surfaces, one [(would)(would not)] expect to see sun pillars or other surface reflection phenomena from raindrops.

10. Rays from drops produce rainbows in circular arcs about the antisolar point, the point opposite the Sun along a line from the Sun through the observer’s eyes. The angle measured where straight lines from the antisolar point and from a point on the primary rainbow meet in the observer’s eye is about 42°. It is about 50° for the secondary bow. Someone claiming to have seen a rainbow ringing the Sun [(could be right)(would actually have seen a halo)].

11. Many raindrops must be involved in order for an observer to see a rainbow. A raindrop must be oriented at an angular width of slightly more than 42° to deliver red to the observer’s eye while another drop must at slightly less than 41° to deliver violet to the same eye at the same instant. Consequently, red is the [(outer)(inner)] color in the arc of a primary rainbow. Millions of raindrops fill in the colors of the rainbow to form the bow that can form a circular arc that sometimes stretches from horizon to horizon under proper rain and sunlight conditions.

Rainbows are produced from light interacting with water drops in the atmosphere.

12. A view of a primary and a secondary rainbow is shown in Figure 5. The anti-solar point, the point opposite the Sun along the line from the Sun through the observer’s eyes, is to the lower right corner off the photo. The rainbow forms on a circular arc about that point. With the Sun in the sky and assuming the observer is on a smooth Earth surface with a sea horizon, the anti-solar point is below the horizon so that less than half of the circle on which a rainbow could be formed would be above the horizon. Here the arc of the more colorful primary rainbow separates the part of the image with the lightest background from the part with the darker background. From the inside of the primary rainbow outwards, the colors range from [(red to violet)(violet to red)].

Figure 5. A double rainbow view.

13. The primary rainbow is formed from the Sun’s rays being refracted upon entering a drop, being reflected within the drop, and then refracted again upon leaving the drop. A secondary rainbow would be formed with an additional reflection inside the drop. A faint portion of the secondary rainbow can be seen in the image, well “outside” of the primary bow. The color sequence in the secondary rainbow is reversed from the primary bow, with reddish hues appearing on the [(inside)(outside)] of the secondary rainbow arc.

A faint reddish-purple coloration sometimes seen inside the primary bow is called a supernumerary bow. “Supernumeraries” are formed as diffraction patterns from the primary bow’s light rays. The darker area between the primary and secondary bows, known as Alexander’s dark band, is produced by the absence of rays being directed in those angles by the reflections.

14. As described earlier in this investigation, light rays may also be reflected and refracted by ice crystals in the atmosphere. Ice crystals interact with light to form halos, as seen in Figure 6. The ring centering on the Sun is a 22-degree halo. The halo is formed by light being refracted through the ice crystals to the observer while the observer looks in the general direction [(away from)(toward)] the light source.

Figure 6. Photograph of a halo.

The atmosphere itself may also refract light to form dramatic optical effects. One may recall the impression that the Sun at sunrise or sunset or the Moon rising or setting seems particularly large. Careful measurement of the angular width of the Sun or Moon shows this is an optical illusion. And, angular measurement of the vertical dimension of the Sun or Moon shows it to be smaller near the horizon than at higher elevations in the sky!

Figure 7, a moonrise, shows the oval shape imparted to the Sun or Moon near the horizon. Rays from the bottom and the top of the Moon’s disk are refracted by differing amounts.

Figure 7. Flattening of Moon’s image.

15. The image shows the Moon just above the horizon distorted from a circular disc. This departure from a circle results from the Moon’s rays traveling through air of varying densities near the Earth’s surface. Light from the lower edge of the Moon’s disk passes through air of greater density (hence lower speed) than light from the upper edge of the Moon’s disk. Consequently, the lower beam undergoes [(less)(more)] refraction, causing the Moon’s lower limb to be elevated more than the upper limb. As the Moon rises higher into the sky and light from across its surface experiences little atmospheric refraction, the Moon’s disk appears more and more circular.

Also of note in the figure is the reddish color of the Moon. Light reaching the observer (or camera) is coming through a relatively long path of atmosphere where the blues and greens of the moonlight are preferentially absorbed or scattered, leaving red to complete the journey. This attenuation of the shorter wavelengths of visible light is the same process that is responsible for red sunsets and sunrises.

Suggestions for further activities: To view images of rainbows, halos, and other optical phenomena, go to http://www.atoptics.co.uk/ () and http://old.meteoros.de/indexe.htm (). (Figures 5 and 7 are from NOAA’s NWS Forecast Office page at Sullivan, WI.)