ATMOSPHERIC PRESSURE IN THE VERTICAL

Objectives:

One of the most important properties of the atmosphere is air pressure. After barometer readings at Earth’s surface are “reduced” or “corrected” to sea level, the resulting air pressure values more often than not still vary from place to place and with time. The principal reason for this unevenness in air pressure arises from the variability of air temperature over distance and time. With otherwise similar conditions, warm air is less dense than cold air. Density variations produced by temperature differences lead to pressure differences in the horizontal throughout the atmosphere.

This investigation simulates special “blocks” to study basic understandings about pressure and pressure differences produced by density variations.

After completing this investigation, you should be able to:

• Explain what air pressure is.
• Explain how variations in air temperature cause differences in air pressure.
• Describe how density contrasts between warm and cold air produce horizontal variations in air pressure at different altitudes in the atmosphere.

Introduction:

To study pressure, we must first define it. Pressure is a force acting on a unit area of surface (e.g., pounds per square inch is a pressure measurement). Air pressure is described as the weight (a force) of an overlying column of air acting on a unit area of horizontal surface. To investigate the concept of pressure we will simulate the use of tall and short “blocks” that weigh the same. One tall block and one short block are shown in Figure 1. Tall blocks are cube-shaped and short blocks have the same size base as the tall blocks but are half as high.

Whether tall or short, the blocks employed in this investigation have the following common characteristics:

a. All blocks have the same weight regardless of the volume they occupy.

b. All blocks have the same size square base.

c. All individual blocks exert the same downward pressure on the surface beneath them (because the equivalent weights are acting on the same size bases).

1. Figure 1 shows one tall red block and one short blue block side-by-side on their square bases on the flat horizontal surface of a table (T). Because both blocks weigh the same (although they have different volumes) and their bases are the same size, the blocks exert [(equal)(unequal)] pressure on the surface of the table.

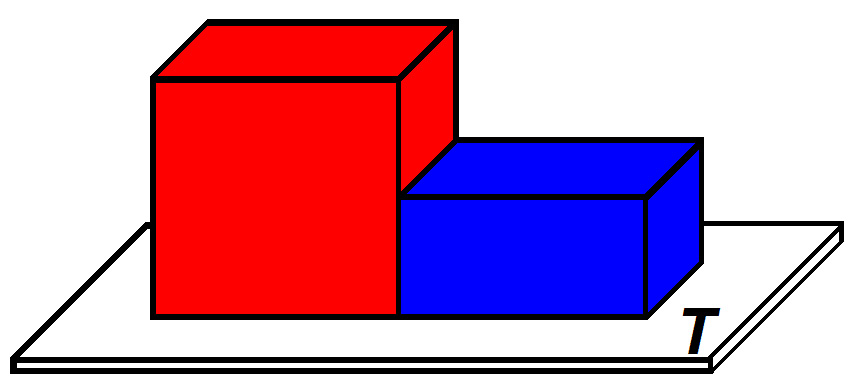
Figure 1. One tall, one short block.

2. The shorter blocks occupy half of the volume of the taller blocks while containing equal masses. (We know their masses are equal because they weigh the same.) Because density is a measurement of mass per unit volume, the smaller blocks are [(twice)(half)] as dense as the larger blocks.

3. In Figure 2, another identical block was placed on top of each block already on the table. The amount of pressure exerted on the table by each stack is [(the same)(twice the)] amount of pressure on the table exerted by the single blocks.

Figure 2. Two tall, two short blocks.

4. The pressure exerted on the table by the tall stack is [(equal)(not equal)] to the pressure exerted on the table by the short stack.

5. As shown in Figure 3, the two stacks are side-by-side with another identical block added to each stack (for a total of 3 blocks in each stack). An imaginary surface (1) has been inserted horizontally through the two stacks so that two shorter blocks and one taller block are positioned beneath the surface. Compare the pressure exerted on the imaginary surface by the overlying blocks. The taller-block stack exerts [(greater)(equal)(less)] pressure on this imaginary surface than does the shorter-block stack.

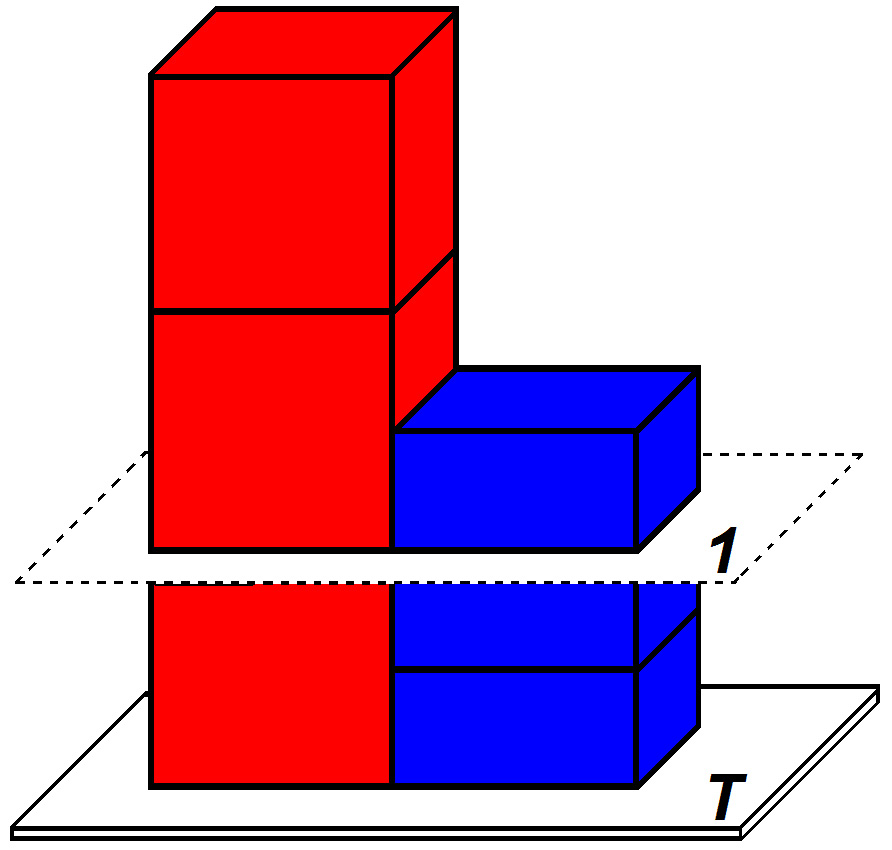
Figure 3. Three tall, three short blocks with surface 1 inserted.

6. Figure 4 shows two more blocks added for a total of five in each stack. A second imaginary horizontal surface (2) is added beneath the top short block and the three top tall blocks. The pressure exerted on the table (T) by the tall stack is [(equal)(unequal)] to the pressure exerted on the table by the short stack.

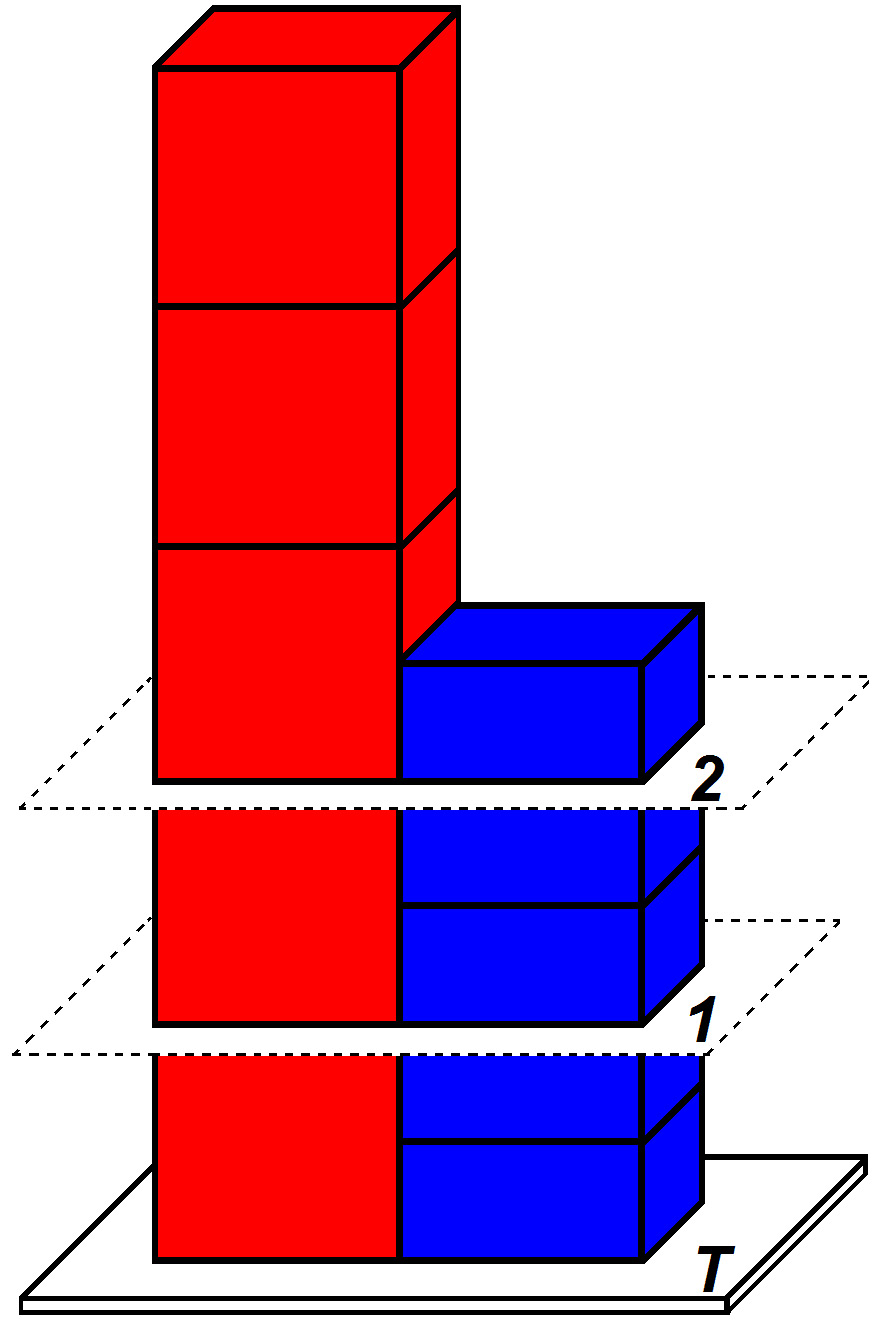
Figure 4. Five tall and short blocks with surfaces 1 and 2 inserted.

7. On the lower imaginary surface (1) in Figure 4, the pressure exerted by all the overlying short blocks is [(one-half)(three-fourths)(the same as)] the pressure exerted by all the overlying tall blocks.

8. On the top imaginary surface (2) in Figure 4, the downward pressure exerted by the overlying short block is [(equal to)(one-half)(one-third)] the pressure exerted by the overlying tall blocks.

9. Starting at the table top and moving upward in Figure 4, the difference in downward pressure on imaginary horizontal surfaces (1 and 2) exerted by the overlying portions of the two stacks [(increases)(decreases)].

10. In the [(taller, less dense)(shorter, more dense)] stack, the pressure decreases more rapidly with height.

11. Look at Figure 5 showing a side view of the two stacks of pressure blocks. It is a view of the same blocks seen in the previous figure. Following the example shown in the lower portion of the figure, draw straight lines connecting the mid-points of bases of blocks exerting the same pressure. These lines connecting equal pressure dots become [(more)(less)] inclined with an increase in height.

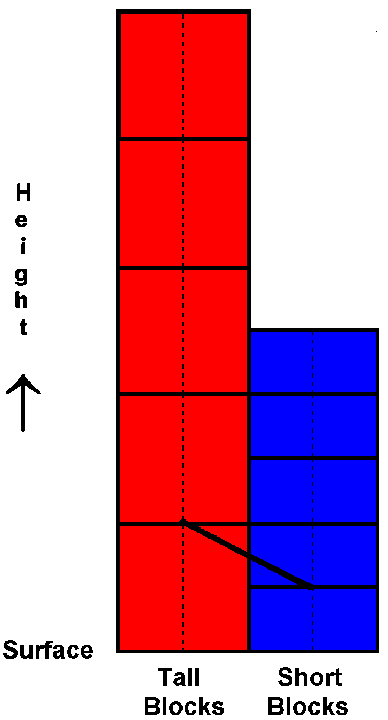
Figure 5. Pressure Blocks, side view.

To this point we have been examining the change in pressure with height in stacks of blocks of different density (short blocks versus tall blocks). Now we apply what we have learned to the rate at which air pressure drops with altitude in the atmosphere.

12. Figure 6, Vertical Cross-Section of Air Pressure, shows a cross-section of the atmosphere based on upper-air soundings obtained by radiosondes simultaneously at Miami, Florida and at Chatham, Massachusetts, approximately 1250 mi. (2010 km) apart at 12Z 26 November 2013. Air pressure values in millibars (mb) are plotted as marks at the altitudes where they were observed, starting with nearly equal values (about 1020 mb) at Earth’s surface. Over Florida, the atmosphere was exerting a pressure of 200 mb at an altitude of approximately [(11,600)(11,800)(12,300)] m above sea level.

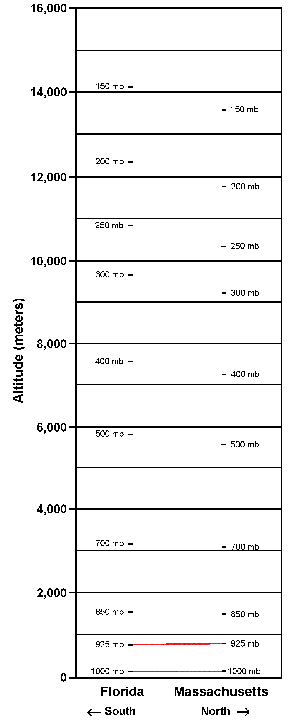
Figure 6. Vertical cross-section of air pressure at 12Z 26 November 2013.

13. The atmosphere above Chatham, Massachusetts was colder and therefore denser than the air above the more southern, warmer air above Miami, Florida. Following the examples shown at the surface and at 925 mb, draw straight lines connecting equal air-pressure dots on the graph. For most of the atmosphere above Earth’s surface these lines representing equal air pressures are [(horizontal)(inclined)].

14. Compare the lines of equal pressure you drew on Figures 5 and 6. They appear quite different because one deals with rigid blocks whereas the other deals with compressible air, and their scales are much different. However, both reveal the effect of density on pressure. The lines of equal pressure generally slope [(upward)(downward)] from the lower-density tall blocks or warm air column above Florida to the higher-density short blocks or cold air column above Massachusetts, respectively.

15. Because of the slope of the equal-pressure lines in Figure 6, it is evident that at 12,300 m above sea level the air pressure in the warmer air over Florida is [(higher than)(the same as)(lower than)] the air pressure in the colder Massachusetts air at the same 12,300-m altitude.

The influence of air temperature on the rate of pressure drop with altitude has important implications for pilots of aircraft that are equipped with air pressure altimeters. An air pressure altimeter is actually a barometer in which altitude is calibrated against air pressure.

16. Imagine that a little before 12Z on 26 November 2013 an aircraft starts its flight from Florida to Massachusetts. At 12Z over Miami, the onboard pressure altimeter indicates that the aircraft is at 5800 meters above sea level. From Figure 6, the air pressure at that altitude over Florida is about [(500)(400)] mb.

17. Relying on the pressure altimeter, the pilot continues to fly toward Massachusetts along a constant pressure level with an indicated altitude of 5800 meters. En route, the air temperature outside the aircraft gradually falls but the pilot does not alter the calibration between air pressure and altitude. Over Massachusetts, the pressure altimeter still reads 5800 meters, the indicated altitude of the aircraft. From Figure 6, however, it is evident that the true altitude of the aircraft over Massachusetts is [(lower than)(the same as)(higher than)] the altitude indicated by the altimeter.

18. The true altitude of the aircraft over Massachusetts is about [(4900)(5500)(5900)] meters.

19. In this example, the aircraft flew along a constant pressure surface (the 500-mb surface) which is at a [(higher)(lower)] altitude in warm air than in cold air. In actual practice, a pilot must adjust the aircraft’s pressure altimeter to correct for changes in the altitude of pressure surfaces due to changes in air temperature en route. This correction ensures a more accurate calibration between air pressure and altitude.

Following the strong frontal system that crossed the country east of the Rocky Mountains as seen in the Applications section of Investigation 5A, cooler air settled into the central and eastern portions of the country. On Tuesday, 8 October 2013, another cool air mass entered the Northwest heading eastward. These invasions of cooler air were beginning to evidence the onset of fall for most of the country.

Radiosonde data can be employed in a variety of ways to provide meteorologists with powerful analytical tools. Data at various atmospheric levels above a station can be plotted as the radiosonde profile on the Stüve diagram that we examined in Investigation 2B. Here we consider atmospheric temperature and pressure conditions above two stations, one located in the cooler air column of the Northwest and one positioned in the southern U.S. that was continuing to experience summer-like warmth. Salem, Oregon was within the column of cold air while Dallas, Texas was experiencing seasonably mild conditions in its air column.

Radiosonde observations at 0000Z 09 OCT 2013 (131009/0000) from Salem (SLE) and Fort Worth-Dallas (FWD) are plotted on Stüve diagrams shown in Figure 7 and Figure 8, respectively. (The Dallas airport with its radiosonde station is located between Fort Worth and Dallas.)

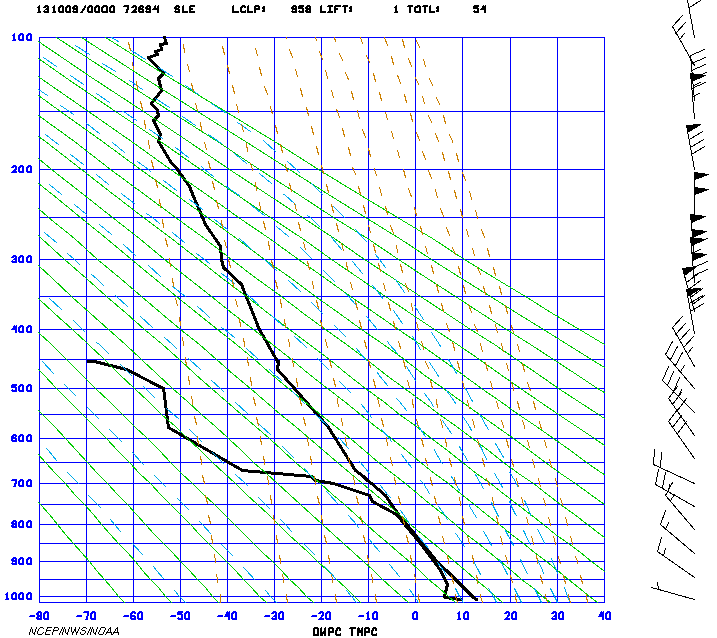
Figure 7. Stüve diagram from Salem, OR (SLE) for 0000Z 09 OCT 2013.

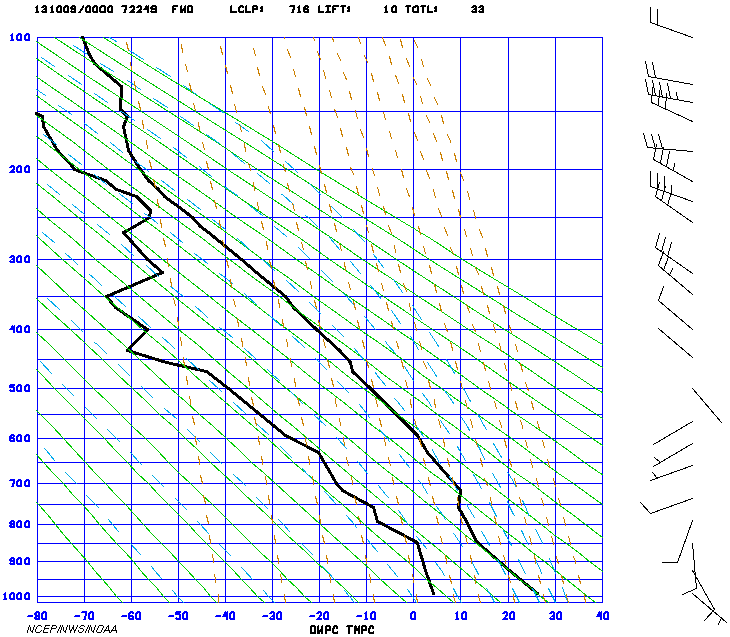
Figure 8. Stüve diagram from Fort Worth – Dallas, TX (FWD) for 0000Z 09 OCT 2013.

20. Note the temperature profiles (heavy solid plotted curves to the right in the Stüve diagrams) for each station. Comparing the two temperature profiles, the atmosphere up to about 260 mb was cooler above [(Dallas)(Salem)]. (Hint: This can be seen by printing copies of the figures and laying one Stüve over the other and holding them up to the light.)

The following table lists a portion of the text data from the two radiosonde observations (complete data for the most recent soundings are available from the course website section, Upper Air, “Upper Air Data - Text”). Pressure levels given below are the so-called “mandatory” levels reported in each station’s sounding plus the surface. The data are presented with the highest pressures at the bottom as is found in the open atmosphere.

Pressure (mb)	Salem (SLE)		Dallas (FWD)
	Temp (°C)	Altitude (m)	Temp (°C)	Altitude (m)
100	–53.5	16250	–70.5	16510
200	–50.7	11810	–58.1	12250
300	–41.3	9110	–36.7	9580
400	–33.3	7110	–20.7	7520
500	–25.7	5530	–9.3	5840
700	–9.5	3009	8.6	3144
850	1.4	1475	13.8	1527
925	6.4	787	20.4	807
992 (FWD sfc)			26.2	171
1009 (SLE sfc)	12.8	61

21. Compare the altitudes of the following pressure levels from the two soundings. The following pressures were at lower altitudes over Dallas (FWD) than over Salem (SLE): [(850 mb)(700 mb)(500 mb)(300 mb)(100 mb)(none of these)].

22. Constant-pressure “surfaces” are those that can be imagined as surfaces in the atmosphere on which the air pressure is everywhere the same, for example, the 500-mb surface. Comparing the altitudes of the pressure surfaces from 925 mb to 100 mb indicates that individual constant-pressure surfaces slope from their altitudes in the generally warmer air over Dallas [(downward)(upward)] to their altitudes in the cooler air over Salem.

23. Assume you wish to fly from Dallas to Salem at a 30,000-foot (9144 m) altitude as indicated by your pressure altimeter. Using a pressure altimeter, you are actually flying along a constant-pressure surface. (To visualize this flight, you can compare the altitudes of the 300-mb levels of the two stations, a pressure that is found near 30,000 feet.) As you approach Salem, your aircraft would actually be at a [(higher)(lower)] altitude than that indicated by your altimeter when you were over Dallas.

24. Conversely, if you were to fly from Dallas to Salem while maintaining an actual altitude of 30,000 feet, the air pressure outside your plane would [(gradually increase)(remain the same)(gradually decrease)].

25. Recall the introductory portion of Investigation 5B where profiles from Miami and Minneapolis over a comparable range of latitude were shown in Figure 6. In general, as one moves toward Earth’s poles and higher latitudes, one would expect the altitudes of a particular constant-pressure surface to become [(higher)(lower)].

26. This altitude change of a given pressure surface as one moves poleward is in response to generally [(higher)(lower)] average temperatures in the underlying air columns regardless of storm systems.

Changes in tropospheric conditions above a station with passing weather systems can be tracked with Stüve diagrams and upper-air maps. This is just one example of the influence of tropospheric temperature contrasts resulting from broad-scale weather systems. As weather systems migrating across the country cause tropospheric changes, try calling up Stüve diagrams from Salem or Dallas from the course website to compare to those seen here. You might also compare quite different stations such as Hilo, Hawaii and Anchorage, Alaska, from the course website or a similar pair of warm/cold locations via the Plymouth State University website linked from the same course Stüve page.