Introduction

This lab will explore streamlining as a utility in identifying different airmasses, zones of convergence and/or fronts, and centers of circulation. Streamlining is useful for this in midlatitudes, and is an especially important process in tropical areas where horizontal temperature and pressure gradients are relatively weak and kinematic processes drive much of the active weather.
Pre-Lab: Definitions & Types of Streamlines
Streamlines are a family of curves that are instantaneously tangent to the velocity vectors in a flow field. They show the direction toward which a fluid element will travel at any point in time.
Streamlines represent the instantaneous direction of the wind and are drawn as unending lines that may converge or diverge from one another (following specific rules). They are drawn at roughly even intervals to capture the flow in all areas. Thus, the distance between streamlines is not generally representative of any gradient or proportional to wind speed.
Pre-Lab: Definitions & Types of Streamlines » Waves
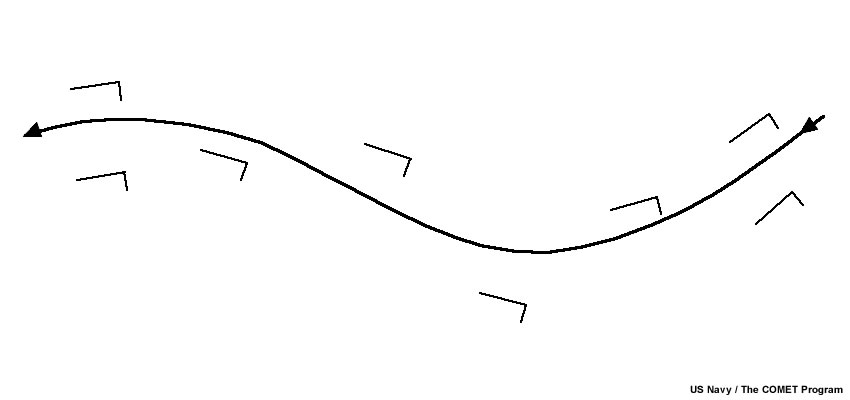
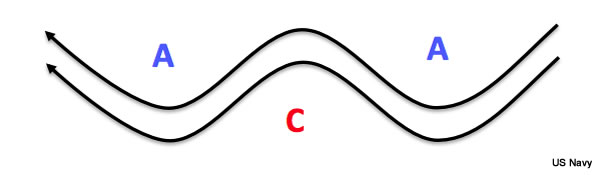
Perhaps the most simple and commonly observed streamline pattern, aside from a straight line, is the wave pattern. A wave is represented by an oscillation, corresponding to regions of alternating cyclonic or anticyclonic flow (lower or higher pressure, respectively). The pattern shown here and throughout rest of lab represent northern hemispheric conditions.
Pre-Lab: Definitions & Types of Streamlines » Asymptotes
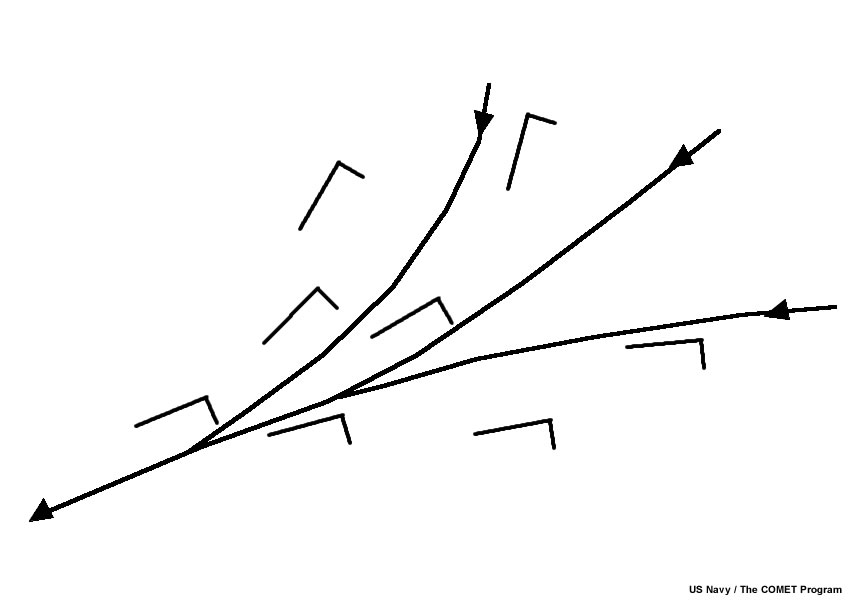
An asymptote is a streamline upon which other streamlines merge or diverge from. When the flow is not a simple wave as above and areas of confluence or diffluence exist, it can often be captured by drawing asymptotes.
A confluent asymptote is a streamline on which other streamlines converge. Confluent asymptotes are commonly analyzed in the vicinity of cyclonic circulations and along fronts, but may also be found elsewhere. See the red streamline below for an example. *Note: red is a standard coloring for indicating confluence/convergence in military streamline analyses, while blue is used for difluence/divergence. Other analysis sources may use these convections, or use all black streamlines.

A diffluent asymptote is a streamline from which other streamlines diverge. diffluent asymptotes are typically analyzed emerging from anticyclonic circulation centers, in flow transitions and in other areas. An example is below.

Pre-Lab: Definitions & Types of Streamlines » Singular Points
Singular points are locations where the direction of flow cannot be determined - that is, more than one approach to a streamline can be drawn. This can be a point on the chart into which more than one streamline enters, or where streamlines might form a closed curve. The wind speed is zero at the singular point, and very light in adjacent areas.
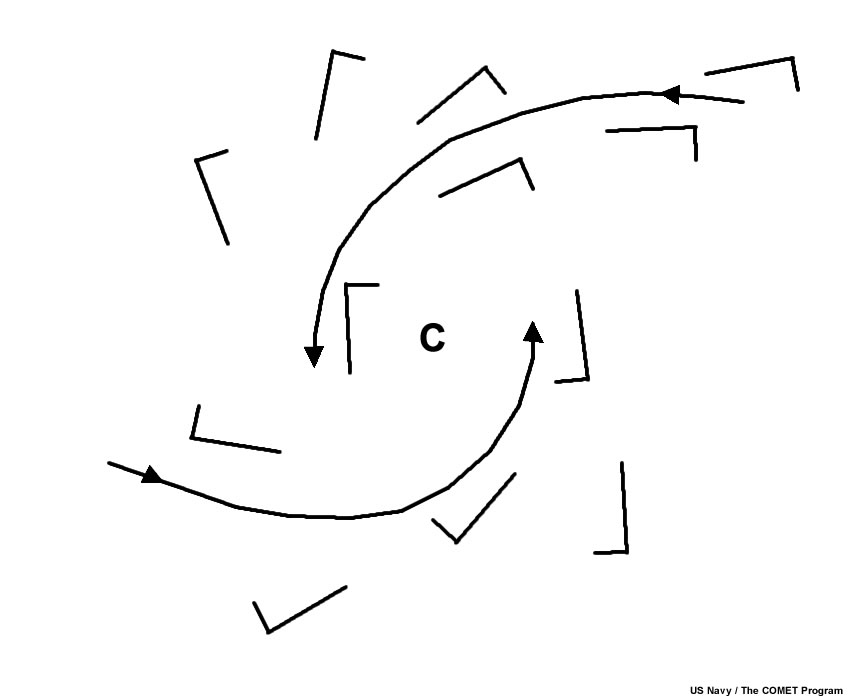
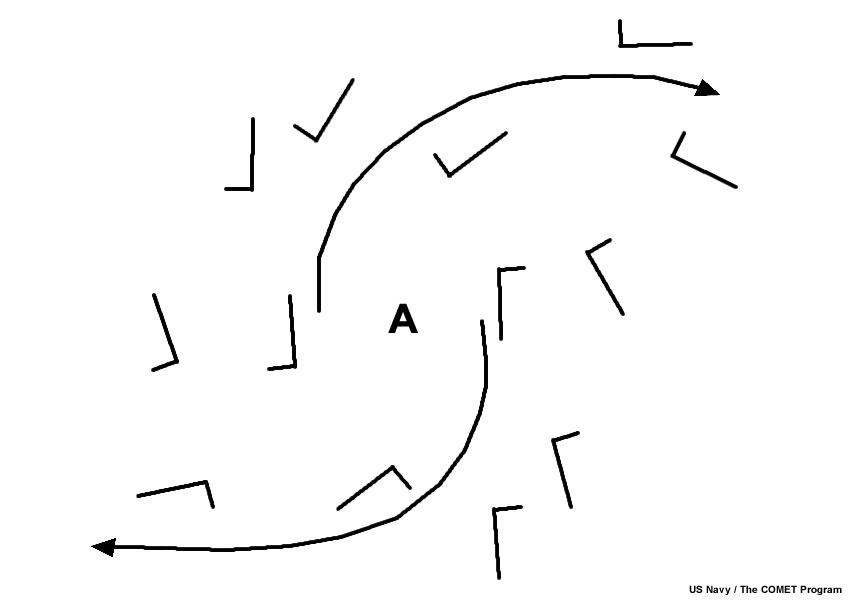
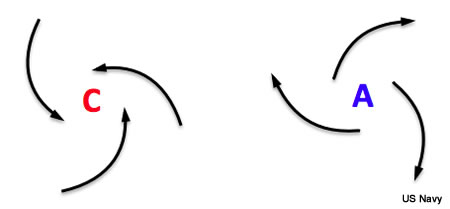
Vortex Singular Points are circulation cells that can be cyclonic or anticyclonic. A cyclonic indraft is indicated as a closed circulation where streamlines converge into low pressure.
An anticyclonic outdraft is a closed circulation center where streamlines diverge out of high pressure. See below for examples of each. Note again the color convention of the letters used to indicate anticyclonic and cyclonic circulations.
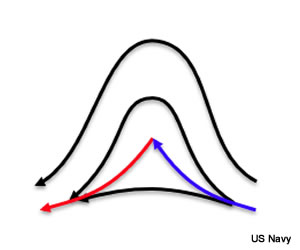
A cusp is an intermediate pattern that represents a transition phase between a wave and a circulation center. Cusps are generally short-lived on the synoptic scale. An example is shown below.
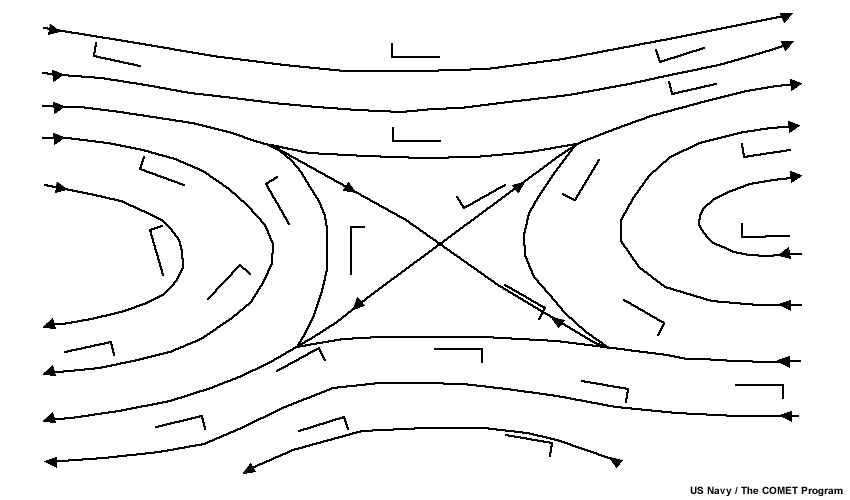
Neutral Singular Points denote locations where confluent and diffluent asymptotes appear to intersect. In some cases, the neutral point captures an area of nearly pure deformation flow, similar to what is shown below with incoming southeasterlies and northwesterlies deforming to produce exiting northeasterlies and southwesterlies.
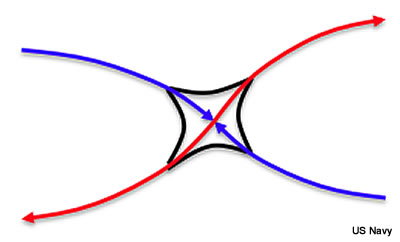
Neutral points are transition areas between two like singular points, or they will separate one flow regime from an adjacent flow regime of the opposite direction (e.g., a large area of midlatitude westerly flow adjacent to a large area of tropical easterly trade winds). Examples of a wave train including neutral points are below.

Another commonly observed pattern (necessarily observed, even) is a neutral point that separates prevailing background flow from the opposite-directed flow within an anticyclone or cyclone. See below for an example of a cyclone embedded in tropical easterlies - a neutral point must separate the background easterly flow from the westerly flow somewhere adjacent to the center of circulation.

Pre-Lab: Definitions & Types of Streamlines » Knowledge Check
Before starting the streamlining process, let's check for understanding and ability to identify the aforementioned patterns and features.
Question 1 of 4
What are the three major features in a streamline analysis? Select all that apply.
The correct answers are a, c and e.
Question 2 of 4
Asymptotes are used in areas of major convergence or divergence
Question 3 of 4
Very briefly describe the wind speed in the center and immediate vicinity of a singular point.
Winds are nearly zero at the center of an indraft/outdraft or neutral point, and are generally light in immediate vicinity
Question
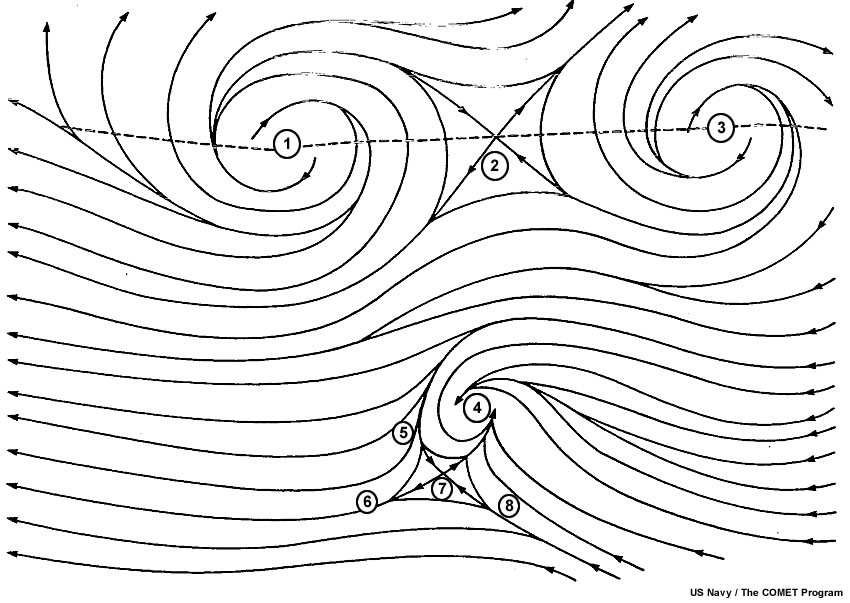
Choose the type of streamline or flow feature that is present at each of the numbered points on the image above.
The correct answers are highlighted in green above. Note that locations 5 and 8 both show diffluent asymptotes - the flow there is diverging out toward the northeast and southwest, to create a line of convergence that runs through locations 6 and 4.
Pre-Lab: Building a Streamline Analysis
Pre-Lab: Building a Streamline Analysis » Basic Approach and Tips
Here are some general guidelines to keep in mind during the streamlining process. Refer to these guidelines when attempting the practice exercises on the next page and during lab.
- Draw streamlines freehand, keeping them parallel to the overall flow
- Streamlines never cross, except at a neutral point
- Draw streamlines at a roughly regular interval, keeping them frequent enough for another user to easily gauge the overall flow in all regions
- Where winds are slow, it may be difficult or impossible to match all observed wind directions
- A neutral point must exist between two like systems (e.g., two anticyclones), large regimes of opposing flow, and where flow within an indraft or outdraft meets the opposing background flow
- A starting point for drawing streamlines is based on the analyst's judgment. It is commonly easiest to begin with centers of circulation, flow transitions (neutral points), and main flow lines
- When beginning any streamline analysis, first look for the overall flow pattern and main features - this is akin to examining the entire area of the map for maxima, minima and troughs before drawing the first isobar when contouring pressure
- Situational awareness: it is most instructive to examine previous streamline analysis from recent hours. Additionally, satellite and radar loops, where available, can help fill in gaps where observations are sparse.
- And last, but not least: for hand analysis, USE A PENCIL FOR INITIAL SKETCHING!
Pre-Lab: Building a Streamline Analysis » Basic Practice
Before beginning a full streamline analysis with real observations over a large domain, it is best to hone skills with some practice exercises. Use the drawing tools below to practice drawing in a few streamlines for asymptotes and centers of circulation. Wind speeds are all 10 knots for simplicity. The completed streamlines are available upon clicking "done".
Question 1 of 6
Analyze a single streamline from west to east using the pen tool below

| Tool: | Tool Size: | Color: |
|---|---|---|
Question 2 of 6
Analyze a diffluent asymptote and at least two other streamlines

| Tool: | Tool Size: | Color: |
|---|---|---|
Question 3 of 6
Analyze a confluent asymptote and at least two other streamlines

| Tool: | Tool Size: | Color: |
|---|---|---|
Question 4 of 6
Analyze a cyclonic indraft using at least two confluent asymptotes

| Tool: | Tool Size: | Color: |
|---|---|---|
Your streamlines should look something like the ones above in black. With more observations extending outward from this indraft, we could pinpoint where the additional streamlines would join the two confluent asymptotes here, but for now this is sufficient.
Question 5 of 6
Analyze a anticyclonic outdraft using at least two diffluent asymptotes

| Tool: | Tool Size: | Color: |
|---|---|---|
Your streamlines should look something like the ones above in black. With more observations extending outward from this outdraft, we could pinpoint where the additional streamlines would diverge from the two diffluent asymptotes here, but for now this is sufficient.
Question 6 of 6
Complete the analysis of flow in vicinity of a neutral point that has been started below. Remember - streamlines are spaced at roughly even intervals!

| Tool: | Tool Size: | Color: |
|---|---|---|
Your streamlines should look something like the ones above in black.
Next Steps: Lab Activity
Now you should be ready to begin streamlining full maps. Three streamlining cases are available below and via the left-hand menu - the first is idealized, and bridges the pre-lab level of difficulty with more complex cases you might see on a daily basis. A second case is surface wind barbs over the continental US - we recommend streamlining the area east of the Rockies. A final case is atmospheric motion vectors overlaid with IR satellite over the western Pacific. See your instructor to determine which cases you will be analyzing for class.