Introduction

Advection is formally defined as the transport of an atmospheric property solely by the mass motion of the atmosphere. It can be expressed in vector notation as

-V · ∇ X

where V is the wind vector, X a scalar atmospheric property, and del is the gradient of the property. Often, especially in synoptic meteorology, advection refers to horizontal advection using only the x and y gradients.

The process of analyzing the presence and strength of positive or negative advection of a scalar is a straightforward one and is the same for all properties. One needs to examine the wind speed and direction, and the gradient of the scalar field. Recall that the gradient of a scalar property is defined as being in the direction of increasing values of said property.

The simplest advection pattern is one of no advection, as shown below.

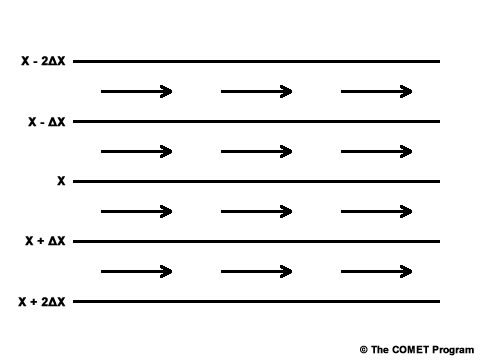
We can see the wind vectors are uniform in speed and direction and are parallel to the scalar field isopleths. Thus, air on the right side of the image is being replaced by air coming from from the left side that possesses exactly the same scalar value. Mathematically, any advection calculation here would result in zero advection because of the 0 degree angle in the dot product.

The next example is one of maximum advection in a uniform wind field. The wind vectors would be perpendicularly oriented to the scalar field like that shown below.

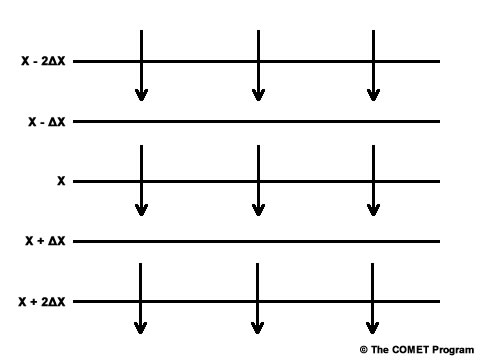
Whether the vectors flow from lower values to higher values or vice versa will tell you the sign of the advection. Here we can see that the lower values at the top of the image will be advected toward the higher values at the bottom. Thus it is a negative advection, similar to what you might see with northerly winds behind a cold front.

Things are rarely this uniform in the everyday atmosphere, so let’s perform some more realistic analyses.