Introduction

Advection is formally defined as the transport of an atmospheric property solely by the mass motion of the atmosphere. It can be expressed in vector notation as

-V · ∇ X

where V is the wind vector, X a scalar atmospheric property, and del is the gradient of the property. Often, especially in synoptic meteorology, advection refers to horizontal advection using only the x and y gradients.

The process of analyzing the presence and strength of positive or negative advection of a scalar is a straightforward one and is the same for all properties. One needs to examine the wind speed and direction, and the gradient of the scalar field. Recall that the gradient of a scalar property is defined as being in the direction of increasing values of said property.

The simplest advection pattern is one of no advection, as shown below.

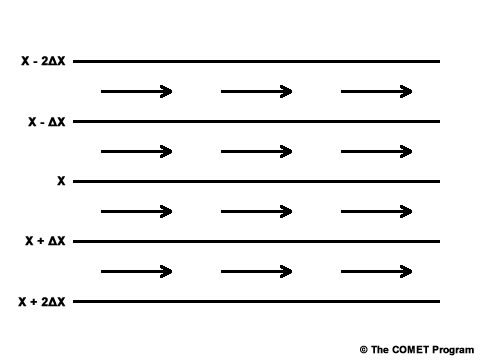
We can see the wind vectors are uniform in speed and direction and are parallel to the scalar field isopleths. Thus, air on the right side of the image is being replaced by air coming from from the left side that possesses exactly the same scalar value. Mathematically, any advection calculation here would result in zero advection because of the 0 degree angle in the dot product.

The next example is one of maximum advection in a uniform wind field. The wind vectors would be perpendicularly oriented to the scalar field like that shown below.

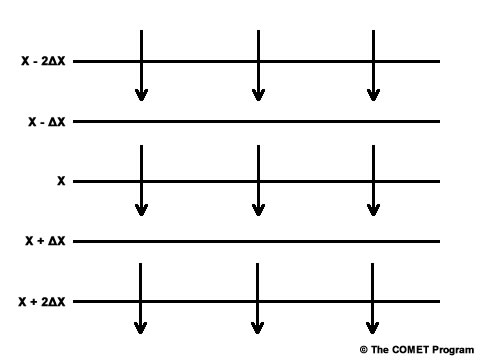
Whether the vectors flow from lower values to higher values or vice versa will tell you the sign of the advection. Here we can see that the lower values at the top of the image will be advected toward the higher values at the bottom. Thus it is a negative advection, similar to what you might see with northerly winds behind a cold front.

Things are rarely this uniform in the everyday atmosphere, so let’s perform some more realistic analyses.

Pre-Lab: Analyzing Advection

The midlatitudes possess greatly varying scalar properties in all dimensions. Another exercise is to modify either the strength of the scalar gradient or the speed of the wind.

Let’s modify our previous example by changing the gradient of X and holding the wind field steady.

What about changing the wind field? Here's an example of the earlier uniform gradient of X with a changing wind field.

Similarly, we can modify the wind speed in the x-direction in the above situation, and we can see that the strength of advection would be highest on the right-hand side of the image where wind vectors are of highest magnitude.

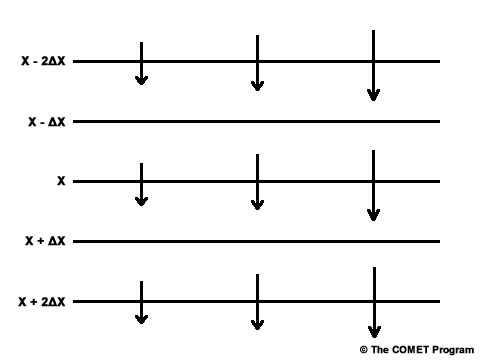
One may notice that even plotted at low density as above, the length of wind vectors can be more difficult to visually interpret than the tightness of the gradient of X.

Another method of quickly and easily assessing the presence and strength of advection is to examine plots of geopotential height and a scalar property.

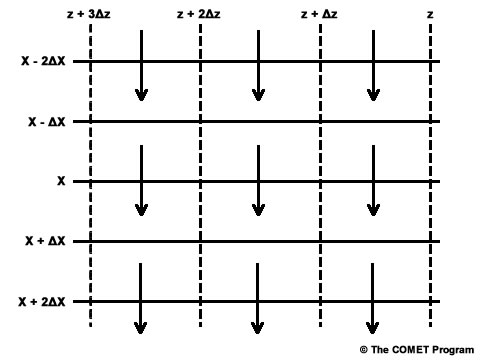
Since the wind is mostly geostrophic above the boundary layer, we can assume that the winds are blowing nearly parallel to the isoheights, for estimation purposes anyway.

The dashed lines here represent the height field associated with these wind vectors. In this manner, one can easily see the boxes (also called solenoids) formed by the intersections of the height and scalar patterns.

Think about what changing the gradient of X or of height would do to the shape and size of the boxes.

Here we can see a shaded graphical representation of the solenoid method. Tightening the height gradient is equivalent to increasing the wind speed, and it has created smaller solenoids, which are shaded in darker gray. Advection is most intense in dark gray. Similarly shaded maps of temperature advection are commonly analyzed in some weather packages.

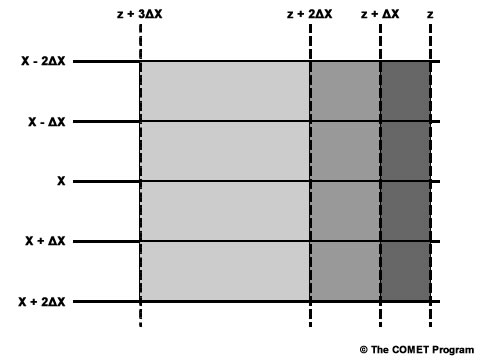
The solenoid method works well for middle and upper level advection analysis, as winds are mostly geostrophic there, with exception of highly curved flow and areas in the immediate vicinity of jetstreaks. Some very important equations, such as those in quasigeostrophic theory, contain geostrophic advection like what we have estimated here.

Now that we've covered the basic ideas behind advection analysis, we'll look at a couple of everyday examples.

Pre-Lab: Practice Analysis

In this section you'll get to practice analyzing advection in a more complicated setting using the drawing tool.

Question 1 of 2

Examine the map of surface isotherms and wind barbs below. Outline areas where cold air advection (CAA) exists in blue. Then, mark the strongest area of CAA with a blue X. Outline areas where warm air advection (WAA) exists in red. Then, mark the strongest area of WAA with a red X. When finished, compare your answer to the solution by clicking done.

Tool:	Tool Size:	Color:
Pen Eraser	36

Firstly, note that warm colors denote positive values of advection (WAA) while cool colors denote CAA. Here we saw a weak temperature gradient across the southeast US that then tightened through the Great Lakes states. Combined with 20 knot wind barbs crossing isotherms at a 70 to 90 degree angle, this indicates strong WAA.

Further west in Iowa and Missouri, there are still strong 20-30 knot southerly winds, but they are mostly parallel to the isotherms there, so advection is slightly cool and weak.

A final location that is seeing some moderate WAA is Arkansas, where the temperature gradient is somewhat tighter and some 10-15 knot wind barbs flow across the isotherms at angles between about 40 and 70 degrees.

Question 2 of 2

Examine the map of 850mb isotherms and isoheights below. Outline areas where cold air advection (CAA) exists in blue. Then, mark the strongest area of CAA with a blue X. Outline areas where warm air advection (WAA) exists in red. Then, mark the strongest area of WAA with a red X. When finished, compare your answer to the solution by clicking done.

Tool:	Tool Size:	Color:
Pen Eraser	36

Here we see that low heights are centered over southern Minnesota. Isotherms are tightly packed in Iowa and extend in this manner southwestward into Kansas and Nebraska. Combined with the strong height gradient associated with the low there, the solenoids are relatively small, indicating stronger advection (in this case CAA, because of the implied wind direction).

Geostrophic winds are blowing mostly parallel to isotherms across parts of Illinois and the Mississippi river valley states, creating weak advection. WAA is present to a moderate degree in a zonal band across southern Wisconsin, Chicago area and southern Michigan where we can again note relatively small solenoids.

Next Steps: Lab Activity

The following imagery is available for lab analysis. This imagery is from the continental US case that is also analyzed in the streamlining and vorticity/deformation ID labs.

The images are large enough to print well on 8.5" by 11" copy paper without resizing, or they can be imported to MS Powerpoint or other software that contains drawing capabilities. The images are from 21Z on March 2.

Consult your instructor for further details on format and which levels are required or recommended.

• Surface Winds Barbs and Temperature
• 850mb Heights and Temperature
• 700mb Heights and Temperature
• 500mb Heights and Absolute Vorticity